Maghanap ng mga break point at ipahiwatig ang kanilang uri. Pag-uuri ng mga punto ng discontinuity ng function

Kahulugan. Hayaang tukuyin ang isang function na f(x) sa ilang pagitan at ang x 0 ay isang punto sa pagitan na ito. Kung , kung gayon ang f(x) ay sinasabing tuloy-tuloy sa puntong x 0 .
Mula sa kahulugan, sumusunod na maaari nating pag-usapan ang tungkol sa pagpapatuloy lamang na may kaugnayan sa mga puntong iyon kung saan tinukoy ang f(x) (kapag tinutukoy ang limitasyon ng isang function, hindi naitakda ang naturang kundisyon). Para sa tuluy-tuloy na pag-andar , ibig sabihin, ang mga operasyong f at lim ay nababago. Ayon sa dalawang kahulugan ng limitasyon ng isang function sa isang punto, maaaring ibigay ang dalawang kahulugan ng pagpapatuloy - "sa wika ng mga pagkakasunud-sunod" at "sa wika ng mga hindi pagkakapantay-pantay" (sa wika ng ε-δ). Iminumungkahi na gawin mo ito sa iyong sarili.
Para sa praktikal na paggamit, kung minsan ay mas maginhawang tukuyin ang pagpapatuloy sa wika ng mga increment.
Ang halagang Δx=x-x 0 ay tinatawag na pagtaas ng argumento, at ang Δy=f(x)-f(x 0) ay ang pagtaas ng function kapag lumilipat mula sa puntong x 0 patungo sa puntong x.
Kahulugan. Hayaang tukuyin ang f(x) sa punto x 0 . Ang isang function na f(x) ay tinatawag na tuloy-tuloy sa isang punto x 0 kung ang isang infinitesimal na pagtaas ng argumento sa puntong ito ay tumutugma sa isang infinitesimal na pagtaas ng function, iyon ay, Δy→0 para sa Δx→0.

Halimbawa 1. Patunayan na ang function na y=sinx ay tuloy-tuloy para sa anumang halaga ng x.
Solusyon. Hayaang ang x 0 ay isang arbitrary na punto. Ang pagbibigay nito ng dagdag na Δx, nakukuha natin ang puntong x=x 0 +Δx. Pagkatapos . Nakukuha namin .
Kahulugan. Ang function na y=f(x) ay tinatawag na tuloy-tuloy sa puntong x 0 sa kanan (kaliwa) kung
.
Ang isang function na tuloy-tuloy sa isang panloob na punto ay parehong kanan at kaliwa tuloy-tuloy. Ang kabaligtaran ay totoo rin: kung ang isang function ay tuluy-tuloy sa isang punto sa kaliwa at kanan, kung gayon ito ay magiging tuluy-tuloy sa puntong iyon. Gayunpaman, ang isang function ay maaari lamang maging tuloy-tuloy sa isang panig. Halimbawa, para sa , , f(1)=1, samakatuwid, ang function na ito ay tuloy-tuloy lamang sa kaliwa (para sa graph ng function na ito, tingnan ang talata 5.7.2 sa itaas).
Kahulugan. Ang isang function ay tinatawag na tuloy-tuloy sa ilang pagitan kung ito ay tuloy-tuloy sa bawat punto ng agwat na ito.
Sa partikular, kung ang agwat ay isang segment, kung gayon ang isang panig na pagpapatuloy ay ipinahiwatig sa mga dulo nito.

Mga katangian ng tuluy-tuloy na pag-andar

1. Ang lahat ng elementarya ay tuluy-tuloy sa kanilang domain ng kahulugan.
2. Kung ang f(x) at φ(x), na ibinigay sa isang tiyak na pagitan, ay tuloy-tuloy sa puntong x 0 ng interval na ito, kung gayon ang mga function ay magiging tuluy-tuloy din sa puntong ito.
3. Kung ang y=f(x) ay tuloy-tuloy sa puntong x 0 mula sa X, at ang z=φ(y) ay tuloy-tuloy sa katumbas na puntong y 0 =f(x 0) mula sa Y, kung gayon ang complex function na z=φ Ang (f(x )) ay magiging tuluy-tuloy sa punto x 0 .

Mga function break at ang kanilang pag-uuri

Ang isang tanda ng pagpapatuloy ng function na f(x) sa puntong x 0 ay ang pagkakapantay-pantay, na nagpapahiwatig ng pagkakaroon ng tatlong kundisyon:
1) ang f(x) ay tinukoy sa punto x 0 ;
2) ;
3) .
Kung hindi bababa sa isa sa mga kinakailangang ito ang nilabag, ang x 0 ay tinatawag na break point ng function. Sa madaling salita, ang break point ay isang punto kung saan ang function na ito ay hindi tuloy-tuloy. Mula sa kahulugan ng mga breakpoint, sumusunod na ang mga breakpoint ng isang function ay:
a) mga puntos na kabilang sa domain ng kahulugan ng function kung saan ang f(x) ay nawawala ang ari-arian ng pagpapatuloy,
b) mga puntos na hindi kabilang sa domain ng kahulugan ng f(x), na mga katabing punto ng dalawang pagitan ng domain ng kahulugan ng function.
Halimbawa, para sa isang function, ang point x=0 ay isang break point, dahil ang function sa puntong ito ay hindi tinukoy, at ang function ay may discontinuity sa puntong x=1, na katabi ng dalawang pagitan (-∞,1) at (1,∞) ng domain ng kahulugan ng f(x) at hindi umiiral.

Ang sumusunod na klasipikasyon ay pinagtibay para sa mga break point.
1) Kung sa puntong x 0 ay may hangganan At , ngunit f(x 0 +0)≠f(x 0 -0), pagkatapos x 0 ay tinatawag discontinuity point ng unang uri , at tinatawag na pagtalon ng function .

Halimbawa 2. Isaalang-alang ang function
Ang function ay maaari lamang masira sa puntong x=2 (sa ibang mga punto ito ay tuloy-tuloy tulad ng anumang polynomial).
Hahanapin natin , . Dahil ang mga one-sided na limitasyon ay may hangganan, ngunit hindi katumbas ng bawat isa, kung gayon sa puntong x=2 ang function ay may discontinuity ng unang uri. Tandaan na , samakatuwid ang function sa puntong ito ay tuloy-tuloy sa kanan (Larawan 2).
2) Mga discontinuity point ng pangalawang uri ay tinatawag na mga punto kung saan ang hindi bababa sa isa sa mga one-sided na limitasyon ay katumbas ng ∞ o wala.

Halimbawa 3. Ang function na y=2 1/ x ay tuloy-tuloy para sa lahat ng value ng x maliban sa x=0. Maghanap tayo ng mga one-sided na limitasyon: , , samakatuwid ang x=0 ay isang discontinuity point ng pangalawang uri (Fig. 3).
3) Point x=x 0 ay tinatawag naaalis na break point , kung f(x 0 +0)=f(x 0 -0)≠f(x 0).
"Aalisin" namin ang puwang sa kahulugan na sapat na upang baguhin (muling tukuyin o muling tukuyin) ang halaga ng function sa puntong ito sa pamamagitan ng pagtatakda , at ang function ay magiging tuluy-tuloy sa puntong x 0 .
Halimbawa 4. Ito ay kilala na , at ang limitasyong ito ay hindi nakadepende sa paraan na ang x ay nagiging zero. Ngunit ang pag-andar sa puntong x=0 ay hindi tinukoy. Kung palawigin natin ang function sa pamamagitan ng pagtatakda ng f(0)=1, ito ay magiging tuloy-tuloy sa puntong ito (sa ibang mga punto ito ay tuloy-tuloy bilang quotient ng tuluy-tuloy na function na sinx at x).
Halimbawa 5. Suriin ang pagpapatuloy ng isang function .
Solusyon. Ang mga function na y=x 3 at y=2x ay tinukoy at tuluy-tuloy sa lahat ng dako, kasama ang mga ipinahiwatig na pagitan. Suriin natin ang junction point ng mga pagitan x=0:
, , . Nakukuha namin iyon , na nagpapahiwatig na sa puntong x=0 ang function ay tuloy-tuloy.
Kahulugan. Ang isang function na tuloy-tuloy sa isang interval maliban sa isang may hangganang bilang ng mga discontinuity point ng unang uri o naaalis na discontinuity ay tinatawag na piecewise continuous sa interval na ito.

Mga halimbawa ng mga di-tuloy na function

Halimbawa 1. Ang function ay tinukoy at tuloy-tuloy sa (-∞+∞) maliban sa puntong x=2. Tukuyin natin ang uri ng pahinga. Since At , pagkatapos ay sa puntong x=2 mayroong isang discontinuity ng pangalawang uri (Larawan 6).
Halimbawa 2. Ang function ay tinukoy at tuloy-tuloy para sa lahat ng x maliban sa x=0, kung saan ang denominator ay zero. Maghanap tayo ng mga one-sided na limitasyon sa puntong x=0:
Ang mga one-sided na limitasyon ay may hangganan at iba, samakatuwid, ang x=0 ay isang discontinuity point ng unang uri (Larawan 7).
Halimbawa 3. Tukuyin kung anong mga punto at kung anong uri ng mga discontinuities mayroon ang function
Ang function na ito ay tinukoy sa [-2,2]. Dahil ang x 2 at 1/x ay tuloy-tuloy sa mga pagitan [-2,0] at , ayon sa pagkakabanggit, ang discontinuity ay maaari lamang mangyari sa junction ng mga pagitan, iyon ay, sa puntong x=0. Dahil ang , kung gayon ang x=0 ay isang discontinuity point ng pangalawang uri.

Halimbawa 4. Posible bang alisin ang mga gaps sa pag-andar:
A) sa puntong x=2;
b) sa puntong x=2;
V) sa punto x=1?
Solusyon. Tungkol sa halimbawa a) maaari nating agad na sabihin na ang discontinuity f(x) sa puntong x=2 ay hindi maaaring alisin, dahil sa puntong ito ay may mga walang katapusang one-sided na limitasyon (tingnan ang halimbawa 1).
b) Ang function na g(x) bagama't may finite one-sided na limitasyon sa puntong x=2

(,),

ngunit hindi sila nagtutugma, kaya hindi rin maalis ang puwang.
c) Ang function na φ(x) sa discontinuity point x=1 ay may katumbas na one-sided finite limits: . Samakatuwid, ang gap ay maaaring alisin sa pamamagitan ng muling pagtukoy sa function sa x=1 sa pamamagitan ng paglalagay ng f(1)=1 sa halip na f(1)=2.

Halimbawa 5. Ipakita na ang Dirichlet function

hindi nagpapatuloy sa bawat punto sa numerical axis.
Solusyon. Hayaang ang x 0 ay anumang punto mula sa (-∞+∞). Sa alinman sa mga kapitbahayan nito ay may parehong makatwiran at hindi makatwiran na mga punto. Nangangahulugan ito na sa anumang kapitbahayan ng x 0 ang function ay magkakaroon ng mga halaga na katumbas ng 0 at 1. Sa kasong ito, ang limitasyon ng function sa puntong x 0 ay hindi maaaring umiral alinman sa kaliwa o sa kanan, na nangangahulugan na ang Dirichlet function ay may mga discontinuities ng pangalawang uri sa bawat punto sa totoong axis.

Halimbawa 6. Maghanap ng mga breakpoint ng function

at tukuyin ang kanilang uri.
Solusyon. Ang mga puntos na pinaghihinalaang nasira ay mga puntos x 1 =2, x 2 =5, x 3 =3.
Sa puntong x 1 =2 f(x) ay may discontinuity ng pangalawang uri, dahil
.
Ang punto x 2 =5 ay isang punto ng pagpapatuloy, dahil ang halaga ng function sa puntong ito at sa paligid nito ay tinutukoy ng pangalawang linya, at hindi ang una: .
Suriin natin ang punto x 3 =3: , , kung saan sumusunod na ang x=3 ay isang discontinuity point ng unang uri.

Para sa malayang desisyon.
Suriin ang mga function para sa continuity at tukuyin ang uri ng mga discontinuity point:
1) ; Sagot: x=-1 – punto ng naaalis na discontinuity;
2) ; Sagot: Discontinuity ng pangalawang uri sa punto x=8;
3) ; Sagot: Discontinuity ng unang uri sa x=1;
4)
Sagot: Sa puntong x 1 =-5 ay may naaalis na puwang, sa x 2 =1 may puwang ng pangalawang uri at sa puntong x 3 =0 ay may puwang ng unang uri.
5) Paano dapat piliin ang numero A upang ang function

magiging tuluy-tuloy sa x=0?
Sagot: A=2.
6) Posible bang piliin ang numero A upang ang function

magiging tuluy-tuloy sa x=2?
Sagot: hindi.

Pagtukoy sa break point ng isang function
Pangwakas na punto x 0 tinawag function break point f (x), kung ang function ay tinukoy sa ilang nabutas na kapitbahayan ng puntong x 0 , ngunit hindi tuloy-tuloy sa puntong ito.

Ibig sabihin, sa discontinuity point, ang function ay alinman sa hindi natukoy o tinukoy, ngunit hindi bababa sa isang one-sided na limitasyon sa puntong ito ay alinman ay wala o hindi katumbas ng halaga ng f (x0) function sa point x 0 .

Tingnan ang "Kahulugan ng pagpapatuloy ng isang function sa isang punto".
Pagpapasiya ng discontinuity point ng 1st kind discontinuity point ng unang uri Tinatawag ang punto
.

, kung ay isang break point at may hangganang one-sided na limitasyon sa kaliwa at kanan:
Kahulugan ng isang function jump Tumalon Δ function
.

sa isang punto ay ang pagkakaiba sa pagitan ng mga limitasyon sa kanan at kaliwa
Pagpapasiya ng discontinuity point ng 1st kind naaalis na break point Pagtukoy sa break point
,
, kung may limitasyon

ngunit ang function sa punto ay alinman sa hindi tinukoy o hindi katumbas ng limitasyong halaga: .

Kaya, ang punto ng naaalis na discontinuity ay ang punto ng discontinuity ng unang uri, kung saan ang pagtalon ng function ay katumbas ng zero.
Pagpapasiya ng discontinuity point ng ika-2 uri Ang breaking point ay tinatawag punto ng discontinuity ng pangalawang uri

, kung hindi ito isang discontinuity point ng 1st kind.

Ibig sabihin, kung walang kahit isang one-sided na limitasyon, o kahit isang one-sided na limitasyon sa isang punto ay katumbas ng infinity.

• Pagsisiyasat ng mga function para sa pagpapatuloy Kapag nag-aaral ng mga function para sa pagpapatuloy, ginagamit namin ang mga sumusunod na katotohanan.
  Mga tungkulin sa elementarya
• at ang kanilang mga kabaligtaran ay tuloy-tuloy sa kanilang domain ng kahulugan. Kabilang dito ang mga sumusunod na function:, pati na rin ang pare-pareho at kabaligtaran na mga pag-andar. Tingnan ang "Sanggunian sa Mga Elementarya na Function".
  Kabuuan, pagkakaiba at produkto dalawang tuloy-tuloy na function sa isang tiyak na hanay ng mga function ay isang tuluy-tuloy na function sa set na ito, maliban sa mga punto kung saan ang denominator ng fraction ay naglalaho. Tingnan ang "Aritmetikong katangian ng tuluy-tuloy na pag-andar"
• Kumplikadong function ay tuloy-tuloy sa isang punto kung ang function ay tuloy-tuloy sa punto at ang function ay tuloy-tuloy sa punto .

Tingnan ang "Limit at pagpapatuloy ng isang kumplikadong function"

Mga halimbawa

Halimbawa 1
.

Ibinigay ang isang function at dalawang halaga ng argumento at .
Ito ay kinakailangan: 1) upang matukoy kung ang function na ito ay tuloy-tuloy o hindi tuloy-tuloy para sa bawat isa sa mga ibinigay na halaga ng argumento; 2) sa kaso ng isang function discontinuity, hanapin ang mga limitasyon nito sa discontinuity point sa kaliwa at kanan, itatag ang uri ng discontinuity; 3) gumawa ng isang eskematiko na pagguhit.
.

Ang ibinigay na function ay kumplikado. Maaari itong tingnan bilang isang komposisyon ng dalawang function: 1 , .
.
Pagkatapos
Isaalang-alang natin ang pag-andar.

Binubuo ito ng isang function at constants gamit ang arithmetic operations ng addition at division. Ang function ay elementarya - isang power function na may exponent
. Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable.

Samakatuwid, ang function ay tinukoy at tuloy-tuloy para sa lahat maliban sa mga punto kung saan ang denominator ng fraction ay naglalaho. Itinakda namin ang denominator na katumbas ng zero at lutasin ang equation:

Kumuha kami ng isang ugat. Kaya, ang function ay tinukoy at tuloy-tuloy para sa lahat maliban sa punto..

Isaalang-alang natin ang pag-andar.

Isa itong exponential function na may positibong exponent base. Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable.
Samakatuwid, ang ibinigay na function ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable maliban sa punto.
,
,
.

Kaya, sa punto , ang ibinigay na function ay tuloy-tuloy.
.
Graph ng function na y =
.

4 1/(x+2)
Samakatuwid, ang ibinigay na function ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable maliban sa punto.
,
,
.

Isaalang-alang natin ang punto.

Sa puntong ito ang function ay hindi tinukoy. Samakatuwid ito ay hindi tuloy-tuloy. Itatag natin ang uri ng pahinga. Para magawa ito, nakakahanap kami ng mga one-sided na limitasyon.
Gamit ang koneksyon sa pagitan ng walang hanggan malaki at napakaliit na function, para sa limitasyon sa kaliwa mayroon kami:
.

sa ,

Dito ginamit namin ang mga sumusunod na karaniwang tinatanggap na mga notasyon:
.

Ginamit din namin ang property ng exponential function na may base:

Katulad nito, para sa limitasyon sa kanan mayroon kaming: 1 .

Ang function na ito ay tinatawag ding linear. Ito ay tinukoy at tuloy-tuloy para sa lahat ng mga halaga ng variable.
, .
Kasama dito ang dalawa pang function: at .

Binubuo ang mga ito ng mga function at constants gamit ang arithmetic operations ng karagdagan at multiplikasyon:

Samakatuwid sila ay tuloy-tuloy din para sa lahat.
.
Dahil ang mga function na kasama sa komposisyon ay tuluy-tuloy para sa lahat, maaari itong magkaroon ng mga discontinuity point lamang sa mga punto ng gluing ng mga bahagi nito. Ito ang mga tuldok at .

Sinusuri namin ang pagpapatuloy sa mga puntong ito. Para magawa ito, makakahanap kami ng mga one-sided na limitasyon.
.
Isaalang-alang natin ang punto.

Upang mahanap ang kaliwang limitasyon ng isang function sa puntong ito, dapat nating gamitin ang mga halaga ng function na ito sa anumang kaliwang butas na kapitbahayan ng punto.
.

Kunin natin ang kapitbahayan.
;
.
sa ibabaw nito.

Kung gayon ang limitasyon sa kaliwa ay:

Dito ginamit namin ang katotohanan na ang function ay tuloy-tuloy sa isang punto (tulad ng sa anumang iba pang punto). Samakatuwid, ang kaliwa nito (pati na rin ang kanan) na limitasyon ay katumbas ng halaga ng function sa puntong ito.

Hanapin natin ang tamang limitasyon sa punto .
.

Upang gawin ito, dapat nating gamitin ang mga halaga ng pag-andar sa anumang tamang butas na kapitbahayan ng puntong ito. Kunin natin ang kapitbahayan.
.
sa ibabaw nito.

Kung gayon ang limitasyon sa kanan ay:
;
;
; .
Dito rin namin sinamantala ang pagpapatuloy ng pag-andar.
.

Dahil, sa punto, ang limitasyon sa kaliwa ay hindi katumbas ng limitasyon sa kanan, kung gayon ang pag-andar dito ay hindi tuloy-tuloy - ito ay isang discontinuity point. Dahil may hangganan ang isang panig na limitasyon, ito ay isang discontinuity point ng unang uri. Mga function ng jump:
.
Ngayon tingnan natin ang punto.
.

Sa parehong paraan, kinakalkula namin ang mga one-sided na limitasyon:
Dahil ang function ay tinukoy sa isang punto at ang kaliwang limitasyon ay katumbas ng tamang limitasyon, kung gayon ang function ay tuloy-tuloy sa puntong ito. .
Ang function ay may discontinuity ng unang uri sa punto .

Tumalon function sa loob nito: .
Sa iba pang mga punto ang function ay tuloy-tuloy. .
Halimbawa 3
Tukuyin ang mga discontinuity point ng function at siyasatin ang katangian ng mga puntong ito kung
Iyon ay, ang mga function at naiiba lamang sa isang punto: ang mga ito ay tinukoy sa , ngunit sa puntong ito ay hindi sila tinukoy.

Upang matukoy ang uri ng mga discontinuity point, kailangan nating hanapin ang mga one-sided na limitasyon ng function sa mga punto at .

Upang kalkulahin ang mga ito, sasamantalahin natin ang katotohanan na kung ang mga halaga ng isang function ay binago, o ginawang hindi natukoy sa isang tiyak na bilang ng mga puntos, kung gayon ito ay hindi magkakaroon ng anumang epekto sa halaga o pagkakaroon ng limitasyon sa isang di-makatwirang punto (tingnan ang "Ang impluwensya ng mga halaga ng function sa isang may hangganan na bilang ng mga puntos sa halaga ng limitasyon "). Iyon ay, ang mga limitasyon ng function sa anumang mga punto ay katumbas ng mga limitasyon ng function.
.
Isaalang-alang natin ang punto.

Ang denominator ng fraction sa function ay hindi napupunta sa zero. Samakatuwid ito ay tinukoy at tuloy-tuloy sa .
;
.
Ito ay sumusunod na mayroong limitasyon sa at ito ay katumbas ng halaga ng function sa puntong ito:

Samakatuwid, ang punto ay isang punto ng isang naaalis na discontinuity ng unang uri.

Isaalang-alang natin ang punto.
Gamit ang koneksyon sa pagitan ng infinitesimal at infinites large function, mayroon tayong:

Dahil ang mga limitasyon ay walang hanggan, mayroong isang discontinuity ng pangalawang uri sa puntong ito.

Ang function ay may naaalis na discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa . Ginamit na panitikan: O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. Matatanggal na puwang. Kahulugan. Dot a tinatawag na naaalis na discontinuity point ng function O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. y=f(x) a, kung ang limitasyon ng function f(x) umiiral sa puntong ito, ngunit sa punto a function

alinman sa hindi tinukoy o may pribadong kahulugan f(a)

, iba sa limitasyon sa puntong ito. Halimbawa . Halimbawa, ang function ay nasa punto

x=0 a naaayos na puwang. Sa katunayan, ang paglilimita ng halaga ng function na ito sa punto O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. x=0 O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. ay katumbas ng 1. Ang bahagyang halaga ay katumbas ng 2. O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. Kung ang function ay nasa punto naaalis na puwang, kung gayon ang puwang na ito ay maaaring alisin nang hindi binabago ang mga halaga ng pag-andar sa mga punto maliban sa . Upang gawin ito, sapat na upang ilagay ang halaga ng function sa punto a katumbas ng halaga ng limitasyon nito sa puntong ito. Kaya, sa halimbawang isinasaalang-alang sa itaas ito ay sapat na upang ilagay sa puntong ito..

f(0)=1

Ang function ay may naaalis na discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa . Ginamit na panitikan: O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. at pagkatapos a, ibig sabihin. function

ay magiging tuluy-tuloy sa punto

alinman sa hindi tinukoy o may pribadong kahulugan Pagkagambala ng unang uri. ay tinatawag na isang discontinuity point ng unang uri kung sa puntong ito ang function naaayos na puwang. Sa katunayan, ang paglilimita ng halaga ng function na ito sa punto sa puntong ito. may hangganan ngunit hindi pantay na kanan at kaliwang limitasyon

alinman sa hindi tinukoy o may pribadong kahulugan Pagkagambala ng unang uri. Magbigay tayo ng ilang halimbawa. . Function y=sgn x . Function pagkalagot ng unang uri. Sa katunayan, at sa gayon ang mga limitasyong ito ay hindi katumbas ng bawat isa.

, tinukoy sa lahat ng dako maliban sa punto

Ang function ay may naaalis na discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa . Ginamit na panitikan: O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. x=1 a ay walang kahit isa sa mga one-sided na limitasyon o kung hindi bababa sa isa sa mga one-sided na limitasyon ay walang katapusan.

alinman sa hindi tinukoy o may pribadong kahulugan Pagkagambala ng unang uri. f(x)=tan x, malinaw naman, ay may discontinuity ng pangalawang uri sa bawat punto x k =π/2+π k, k=0, ± 1, ± 2,…, dahil sa bawat ganoong punto

alinman sa hindi tinukoy o may pribadong kahulugan. Ang function ay may discontinuity ng pangalawang uri sa punto sa puntong ito., dahil sa puntong ito wala itong mga limitasyon sa kanan o kaliwa.

Pagpapatuloy ng isang function sa isang segment

Ang function ay may naaalis na discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa .. Tinukoy ang function sa isang agwat at tuloy-tuloy sa bawat punto nito ay tinatawag na tuloy-tuloy sa bahaging ito.

Bukod dito, sa ilalim ng pagpapatuloy sa punto O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. ay nauunawaan bilang pagpapatuloy sa kanan, at sa pamamagitan ng pagpapatuloy sa isang punto b- pagpapatuloy sa kaliwa.

Sasabihin namin na ang function Kahulugan, tinukoy sa set (x) umabot sa itaas (ibabang) gilid nito , kung mayroong ganoong punto x 0 ∈(x), Ano f(x 0)=β (f(x 0)=α).

[Weierstrass] Teorama. Ang bawat function na tuloy-tuloy sa isang interval ay may hangganan at umabot sa itaas na hangganan nito at sa ibabang hangganan nito.

Theorem [Bolzano-Cauchy]. Kung ang function Kahulugan tuloy-tuloy sa segment At f(a)=A, f(b)=B, pagkatapos ay para sa alinman C, nagtapos sa pagitan ng A At B, may ganyang punto ξ∈ , Ano f(ξ)=C.

Sa madaling salita, ang isang function na tuluy-tuloy sa isang pagitan, kumukuha ng anumang dalawang halaga, ay tumatagal din ng anumang halaga na nasa pagitan ng mga ito.

Bunga. Kung ang isang function ay tuloy-tuloy sa isang segment at kumukuha ng mga halaga ng iba't ibang mga palatandaan sa mga dulo nito, pagkatapos ay mayroong kahit isang punto sa segment na ito kung saan ang function ay naglalaho.

Bunga. Hayaan ang function Kahulugan tuloy-tuloy sa segment At , . Pagkatapos ang function a kinukuha ang lahat ng value mula sa segment at ang mga halagang ito lamang.

Kaya, ang hanay ng lahat ng mga halaga ng isang function na ibinibigay at tuloy-tuloy sa isang partikular na segment ay isa ring segment.

Pagpapatuloy ng pag-andar. Mga breaking points.

Ang toro ay lumalakad, umiindayog, bumuntong-hininga habang siya ay lumalakad:
- Oh, ang board ay nauubusan, ngayon ako ay babagsak!

Sa araling ito susuriin natin ang konsepto ng pagpapatuloy ng isang function, ang pag-uuri ng mga discontinuity point at isang karaniwang praktikal na problema pagpapatuloy ng pag-aaral ng mga pag-andar. Mula sa mismong pangalan ng paksa, maraming intuitively na hulaan kung ano ang tatalakayin at iniisip na ang materyal ay medyo simple. Ito ay totoo. Ngunit ito ay mga simpleng gawain na kadalasang pinaparusahan para sa kapabayaan at isang mababaw na diskarte sa paglutas ng mga ito. Samakatuwid, inirerekumenda ko na pag-aralan mo ang artikulo nang maingat at mahuli ang lahat ng mga subtleties at diskarte.

Ano ang kailangan mong malaman at magagawa? Hindi masyado. Upang matutunan nang mabuti ang aralin, kailangan mong maunawaan kung ano ito limitasyon ng isang function. Para sa mga mambabasa na may mababang antas ng paghahanda, sapat na upang maunawaan ang artikulo Mga limitasyon sa pag-andar. Mga halimbawa ng solusyon at tingnan ang geometric na kahulugan ng limitasyon sa manwal Mga graph at katangian ng elementarya na pag-andar. Maipapayo rin na maging pamilyar ka geometric na pagbabagong-anyo ng mga graph, dahil ang pagsasanay sa karamihan ng mga kaso ay nagsasangkot ng pagbuo ng isang guhit. Ang mga prospect ay optimistiko para sa lahat, at kahit isang buong takure ay makakayanan ang gawain nang mag-isa sa susunod na oras o dalawa!

Pagpapatuloy ng pag-andar. Mga breakpoint at ang kanilang pag-uuri

Konsepto ng pagpapatuloy ng pag-andar

Isaalang-alang natin ang ilang function na tuluy-tuloy sa buong linya ng numero:

O, upang ilagay ito sa mas maikli, ang aming function ay tuloy-tuloy sa (ang hanay ng mga tunay na numero).

Ano ang “philistine” criterion ng pagpapatuloy? Malinaw, ang graph ng isang tuluy-tuloy na function ay maaaring iguhit nang hindi inaangat ang lapis mula sa papel.

Sa kasong ito, dapat na malinaw na makilala ang dalawang simpleng konsepto: domain ng isang function At pagpapatuloy ng pag-andar. Sa pangkalahatan hindi ito ang parehong bagay. Halimbawa:

Ang function na ito ay tinukoy sa buong linya ng numero, iyon ay, para sa lahat Ang kahulugan ng "x" ay may sariling kahulugan ng "y". Sa partikular, kung , pagkatapos . Tandaan na ang isa pang punto ay may bantas, dahil sa pamamagitan ng kahulugan ng isang function, ang halaga ng argument ay dapat na tumutugma sa ang tanging bagay halaga ng function. kaya, domain ng kahulugan ang aming function: .

Gayunpaman ang function na ito ay hindi tuloy-tuloy sa ! Halatang halata na sa puntong naghihirap siya gap. Ang termino ay medyo naiintindihan at nakikita, dito ang lapis ay kailangang mapunit pa rin ang papel. Maya-maya ay titingnan natin ang pag-uuri ng mga breakpoint.

Pagpapatuloy ng isang function sa isang punto at sa isang pagitan

Sa isang partikular na problema sa matematika, maaari nating pag-usapan ang tungkol sa pagpapatuloy ng isang function sa isang punto, ang pagpapatuloy ng isang function sa isang interval, isang kalahating pagitan, o ang pagpapatuloy ng isang function sa isang segment. Ibig sabihin, walang "patuloy lang"– ang pag-andar ay maaaring tuluy-tuloy sa SAAN. At ang pangunahing "building block" ng lahat ng iba pa ay pagpapatuloy ng pag-andar sa punto .

Ang teorya ng mathematical analysis ay nagbibigay ng isang kahulugan ng pagpapatuloy ng isang function sa isang punto gamit ang "delta" at "epsilon" na mga kapitbahayan, ngunit sa pagsasanay ay may ibang kahulugan na ginagamit, kung saan kami ay magbibigay-pansin.

Tandaan muna natin isang panig na mga limitasyon na sumambulat sa ating buhay sa unang aralin tungkol sa mga function graph. Isaalang-alang ang pang-araw-araw na sitwasyon:

Kung lalapit tayo sa axis sa punto umalis(pulang arrow), pagkatapos ay ang kaukulang mga halaga ng "mga laro" ay pupunta sa axis hanggang sa punto (crimson arrow). Sa matematika, ang katotohanang ito ay naayos gamit kaliwang limitasyon:

Bigyang-pansin ang entry (nagbabasa ng "x tends to ka sa kaliwa"). Ang "additive" na "minus zero" ay sumisimbolo , mahalagang nangangahulugan ito na papalapit na tayo sa numero mula sa kaliwang bahagi.

Katulad nito, kung lalapit ka sa puntong "ka" tama(asul na arrow), pagkatapos ay ang "mga laro" ay darating sa parehong halaga, ngunit kasama ang berdeng arrow, at limitasyon sa kanang kamay ay mai-format tulad ng sumusunod:

Ang "Additive" ay sumisimbolo , at ang nakasulat sa entry ay: “x tends to ka on the right.”

Kung ang mga one-sided na limitasyon ay may hangganan at pantay(tulad ng sa aming kaso): , tapos sasabihin natin na may GENERAL limit. Ito ay simple, ang pangkalahatang limitasyon ay ang aming "karaniwan" limitasyon ng isang function, katumbas ng isang may hangganang numero.

Tandaan na kung hindi tinukoy ang function sa (ilabas ang itim na tuldok sa sangay ng graph), mananatiling wasto ang mga kalkulasyon sa itaas. Tulad ng nabanggit nang maraming beses, lalo na sa artikulo sa infinitesimal functions, ibig sabihin ng mga expression na "x" malapit nang walang katapusan lumalapit sa punto, habang HINDI MAHALAGA, kung ang function mismo ay tinukoy sa isang naibigay na punto o hindi. Ang isang magandang halimbawa ay makikita sa susunod na talata, kapag ang function ay nasuri.

Ang function ay may naaalis na discontinuity point ng unang uri sa , at isang discontinuity point ng pangalawang uri sa .: ang isang function ay tuloy-tuloy sa isang punto kung ang limitasyon ng function sa isang naibigay na punto ay katumbas ng halaga ng function sa puntong iyon: .

Ang kahulugan ay detalyado sa mga sumusunod na termino:

1) Ang function ay dapat na tinukoy sa punto, iyon ay, ang halaga ay dapat na umiiral.

2) Dapat mayroong pangkalahatang limitasyon ng function. Tulad ng nabanggit sa itaas, ito ay nagpapahiwatig ng pagkakaroon at pagkakapantay-pantay ng isang panig na mga limitasyon: .

3) Ang limitasyon ng function sa isang naibigay na punto ay dapat na katumbas ng halaga ng function sa puntong ito: .

Kung nilabag kahit isa ng tatlong kundisyon, pagkatapos ay mawawalan ng function ang property ng continuity sa punto .

Pagpapatuloy ng isang function sa isang pagitan ay binuo nang matalino at napakasimple: ang isang function ay tuloy-tuloy sa pagitan kung ito ay tuloy-tuloy sa bawat punto ng ibinigay na pagitan.

Sa partikular, maraming mga pag-andar ang tuluy-tuloy sa isang walang katapusang pagitan, iyon ay, sa hanay ng mga tunay na numero. Ito ay isang linear function, polynomials, exponential, sine, cosine, atbp. At sa pangkalahatan, anumang elementarya function tuloy-tuloy sa nito domain ng kahulugan, halimbawa, ang isang logarithmic function ay tuloy-tuloy sa pagitan . Sana sa ngayon ay mayroon kang magandang ideya kung ano ang hitsura ng mga graph ng mga pangunahing pag-andar. Ang mas detalyadong impormasyon tungkol sa kanilang pagpapatuloy ay maaaring makuha mula sa isang mabait na lalaki na nagngangalang Fichtenholtz.

Sa pagpapatuloy ng isang function sa isang segment at kalahating pagitan, hindi rin mahirap ang lahat, ngunit mas angkop na pag-usapan ito sa klase tungkol sa paghahanap ng minimum at maximum na halaga ng isang function sa isang segment, ngunit sa ngayon ay huwag nating alalahanin ito.

Pag-uuri ng mga break point

Ang kamangha-manghang buhay ng mga pag-andar ay mayaman sa lahat ng uri ng mga espesyal na punto, at ang mga break point ay isa lamang sa mga pahina ng kanilang talambuhay.

Tandaan : kung sakali, magtatalakay ako sa isang elementarya: ang breaking point ay palaging iisang punto– walang "ilang break point sa isang hilera", ibig sabihin, walang ganoong bagay bilang "break interval".

Ang mga puntong ito, sa turn, ay nahahati sa dalawang malalaking grupo: ruptures ng unang uri At ruptures ng pangalawang uri. Ang bawat uri ng puwang ay may sariling katangian, na titingnan natin ngayon:

Discontinuity point ng unang uri

Kung ang kondisyon ng pagpapatuloy ay nilabag sa isang punto at isang panig na mga limitasyon may hangganan , pagkatapos ito ay tinatawag na discontinuity point ng unang uri.

Magsimula tayo sa pinaka-optimistikong kaso. Ayon sa orihinal na ideya ng aralin, nais kong sabihin ang teorya "sa pangkalahatang mga termino," ngunit upang maipakita ang katotohanan ng materyal, nanirahan ako sa pagpipilian na may mga tiyak na character.

Ito ay malungkot, tulad ng isang larawan ng mga bagong kasal sa backdrop ng Eternal Flame, ngunit ang sumusunod na kuha ay karaniwang tinatanggap. Ilarawan natin ang graph ng function sa drawing:


Ang function na ito ay tuloy-tuloy sa buong linya ng numero, maliban sa punto. At sa katunayan, ang denominator ay hindi maaaring katumbas ng zero. Gayunpaman, alinsunod sa kahulugan ng limitasyon, magagawa natin malapit nang walang katapusan lapitan ang "zero" pareho mula sa kaliwa at mula sa kanan, iyon ay, umiiral ang isang panig na mga limitasyon at, malinaw naman, nag-tutugma:
(Kondisyon No. 2 ng pagpapatuloy ay nasiyahan).

Ngunit ang pag-andar ay hindi tinukoy sa punto, samakatuwid, ang Kondisyon Blg. 1 ng pagpapatuloy ay nilabag, at ang pag-andar ay dumaranas ng discontinuity sa puntong ito.

Isang pahinga ng ganitong uri (na may umiiral na pangkalahatang limitasyon) ay tinatawag naaayos na puwang. Bakit matatanggal? Dahil ang function ay maaari muling tukuyin sa break point:

Parang kakaiba? Siguro. Ngunit ang gayong notasyon ng pag-andar ay hindi sumasalungat sa anuman! Ngayon ang puwang ay sarado at lahat ay masaya:


Magsagawa tayo ng isang pormal na pagsusuri:

2) – mayroong pangkalahatang limitasyon;
3)

Kaya, ang lahat ng tatlong mga kondisyon ay nasiyahan, at ang function ay tuloy-tuloy sa isang punto sa pamamagitan ng kahulugan ng pagpapatuloy ng isang function sa isang punto.

Gayunpaman, maaaring tukuyin ng mga matan haters ang function sa isang masamang paraan, halimbawa :


Ito ay kagiliw-giliw na ang unang dalawang kondisyon ng pagpapatuloy ay nasiyahan dito:
1) - ang function ay tinukoy sa isang naibigay na punto;
2) – may pangkalahatang limitasyon.

Ngunit ang ikatlong hangganan ay hindi naipasa: , iyon ay, ang limitasyon ng pag-andar sa punto hindi pantay ang halaga ng isang ibinigay na function sa isang naibigay na punto.

Kaya, sa isang punto ang pag-andar ay dumaranas ng isang discontinuity.

Ang pangalawa, mas malungkot na kaso ay tinatawag pagkalagot ng unang uri na may pagtalon. At ang kalungkutan ay dulot ng isang panig na mga limitasyon na iyon may hangganan at naiiba. Ang isang halimbawa ay ipinapakita sa ikalawang guhit ng aralin. Ang ganitong puwang ay kadalasang nangyayari sa piecewise tinukoy na mga function, na nabanggit na sa artikulo tungkol sa mga pagbabago sa graph.

Isaalang-alang ang piecewise function at tatapusin natin ang pagguhit nito. Paano bumuo ng isang graph? Napakasimple. Sa isang kalahating pagitan ay gumuhit kami ng isang fragment ng isang parabola (berde), sa isang pagitan - isang tuwid na linya ng segment (pula) at sa isang kalahating pagitan - isang tuwid na linya (asul).

Bukod dito, dahil sa hindi pagkakapantay-pantay, ang halaga ay tinutukoy para sa quadratic function (berdeng tuldok), at dahil sa hindi pagkakapantay-pantay, ang halaga ay tinutukoy para sa linear function (asul na tuldok):

Sa pinakamahirap na kaso, dapat kang gumamit ng point-by-point construction ng bawat piraso ng graph (tingnan ang unang aralin tungkol sa mga graph ng mga function).

Ngayon ay magiging interesado lamang tayo sa punto. Suriin natin ito para sa pagpapatuloy:

2) Kalkulahin natin ang mga one-sided na limitasyon.

Sa kaliwa mayroon kaming pulang linyang segment, kaya ang kaliwang bahagi na limitasyon ay:

Sa kanan ay ang asul na tuwid na linya, at ang kanang-kamay na limitasyon:

Bilang resulta, natanggap namin may hangganan na mga numero, at sila hindi pantay. Dahil one-sided na limitasyon may hangganan at naiiba: , pagkatapos ay nagpapaubaya ang aming function discontinuity ng unang uri na may isang pagtalon.

Ito ay lohikal na ang puwang ay hindi maaaring alisin - ang pag-andar ay talagang hindi maaaring higit pang tukuyin at "nakadikit", tulad ng sa nakaraang halimbawa.

Mga discontinuity point ng pangalawang uri

Karaniwan, ang lahat ng iba pang mga kaso ng rupture ay matalinong inuri sa kategoryang ito. Hindi ko ilista ang lahat, dahil sa pagsasagawa, sa 99% ng mga problema ay makakaharap mo walang katapusang agwat– kapag kaliwete o kanang kamay, at mas madalas, ang parehong mga limitasyon ay walang katapusan.

At, siyempre, ang pinaka-halatang larawan ay ang hyperbola sa point zero. Narito ang parehong isang panig na limitasyon ay walang katapusan: , samakatuwid, ang pag-andar ay dumaranas ng discontinuity ng pangalawang uri sa punto .

Sinusubukan kong punan ang aking mga artikulo ng magkakaibang nilalaman hangga't maaari, kaya tingnan natin ang graph ng isang function na hindi pa nakakaharap:

ayon sa karaniwang pamamaraan:

1) Ang function ay hindi tinukoy sa puntong ito dahil ang denominator ay napupunta sa zero.

Siyempre, maaari nating tapusin kaagad na ang pag-andar ay dumaranas ng discontinuity sa punto , ngunit mainam na pag-uri-uriin ang likas na katangian ng discontinuity, na kadalasang kinakailangan ng kundisyon. Upang gawin ito:

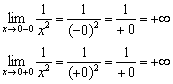
Ipaalala ko sa iyo na sa pamamagitan ng pag-record ang ibig naming sabihin infinitesimal na negatibong numero, at sa ilalim ng entry - infinitesimal positive number.

Ang mga one-sided na limitasyon ay walang katapusan, na nangangahulugan na ang function ay dumaranas ng discontinuity ng 2nd uri sa punto . Ang y-axis ay patayong asymptote para sa graph.

Karaniwang umiral ang magkabilang panig na mga limitasyon, ngunit isa lamang sa mga ito ang walang hanggan, halimbawa:

Ito ang graph ng function.

Sinusuri namin ang punto para sa pagpapatuloy:

1) Ang function ay hindi tinukoy sa puntong ito.

2) Kalkulahin natin ang mga one-sided na limitasyon:

Pag-uusapan natin ang tungkol sa paraan ng pagkalkula ng gayong mga one-sided na limitasyon sa huling dalawang halimbawa ng lektura, bagaman maraming mga mambabasa ang nakakita at nahulaan ang lahat.

Ang limitasyon sa kaliwang kamay ay may hangganan at katumbas ng zero (kami ay "hindi pumunta sa mismong punto"), ngunit ang kanang-kamay na limitasyon ay walang hanggan at ang orange na sangay ng graph ay lumalapit nang walang hanggan malapit sa kanyang patayong asymptote, na ibinigay ng equation (itim na tuldok na linya).

Kaya naghihirap ang pag-andar pangalawang uri ng discontinuity sa puntong .

Tulad ng para sa isang discontinuity ng unang uri, ang function ay maaaring tukuyin sa mismong discontinuity point. Halimbawa, para sa isang piecewise function Huwag mag-atubiling maglagay ng itim na bold na tuldok sa pinanggalingan ng mga coordinate. Sa kanan ay isang sangay ng hyperbola, at ang kanang-kamay na limitasyon ay walang hanggan. Sa tingin ko halos lahat ay may ideya kung ano ang hitsura ng graph na ito.

Ano ang inaabangan ng lahat:

Paano suriin ang isang function para sa pagpapatuloy?

Ang pag-aaral ng isang function para sa pagpapatuloy sa isang punto ay isinasagawa ayon sa isang naitatag na nakagawiang pamamaraan, na binubuo ng pagsuri sa tatlong mga kondisyon ng pagpapatuloy:

Halimbawa 1

I-explore ang function

Solusyon:

1) Ang tanging punto sa loob ng saklaw ay kung saan hindi tinukoy ang function.

2) Kalkulahin natin ang mga one-sided na limitasyon:

Ang mga one-sided na limitasyon ay may hangganan at pantay.

Kaya, sa puntong ang pag-andar ay dumaranas ng isang naaalis na pagkakahinto.

Ano ang hitsura ng graph ng function na ito?

Gusto kong gawing simple , at tila isang ordinaryong parabola ang nakuha. PERO ang orihinal na function ay hindi tinukoy sa point , kaya ang sumusunod na sugnay ay kinakailangan:

Gawin natin ang pagguhit:

Sagot: ang function ay tuloy-tuloy sa buong linya ng numero maliban sa punto kung saan ito ay dumaranas ng naaalis na discontinuity.

Ang pag-andar ay maaaring higit pang tukuyin sa isang mahusay o hindi napakahusay na paraan, ngunit ayon sa kondisyon na ito ay hindi kinakailangan.

Sinasabi mo na ito ay isang malayong halimbawa? Hindi naman. Ito ay nangyari dose-dosenang beses sa pagsasanay. Halos lahat ng mga gawain ng site ay nagmula sa tunay na independiyenteng trabaho at mga pagsubok.

Alisin natin ang ating mga paboritong module:

Halimbawa 2

I-explore ang function para sa pagpapatuloy. Tukuyin ang katangian ng mga discontinuities ng function, kung mayroon sila. Isagawa ang pagguhit.

Solusyon: Para sa ilang kadahilanan, ang mga mag-aaral ay natatakot at hindi gusto ang mga function na may isang module, kahit na walang kumplikado tungkol sa mga ito. Medyo na-touch na natin ang mga ganoong bagay sa aralin. Mga pagbabagong geometriko ng mga graph. Dahil ang modyul ay hindi negatibo, ito ay pinalawak tulad ng sumusunod: , kung saan ang "alpha" ay ilang expression. Sa kasong ito, at ang aming function ay dapat na nakasulat nang paisa-isa:

Ngunit ang mga praksyon ng parehong piraso ay dapat bawasan ng . Ang pagbawas, tulad ng sa nakaraang halimbawa, ay hindi magaganap nang walang mga kahihinatnan. Ang orihinal na function ay hindi tinukoy sa punto dahil ang denominator ay napupunta sa zero. Samakatuwid, dapat ding tukuyin ng system ang kundisyon , at gawing mahigpit ang unang hindi pagkakapantay-pantay:

Ngayon tungkol sa isang NAPAKAKINABANGANG diskarte sa pagpapasya: bago tapusin ang gawain sa isang draft, kapaki-pakinabang na gumawa ng isang pagguhit (hindi alintana kung ito ay kinakailangan ng mga kondisyon o hindi). Makakatulong ito, una, upang agad na makita ang mga punto ng pagpapatuloy at mga punto ng hindi pagkakatuloy, at, pangalawa, ito ay 100% na mapoprotektahan ka mula sa mga error kapag naghahanap ng isang panig na mga limitasyon.

Gawin natin ang pagguhit. Alinsunod sa aming mga kalkulasyon, sa kaliwa ng punto ay kinakailangan upang gumuhit ng isang fragment ng isang parabola (asul na kulay), at sa kanan - isang piraso ng isang parabola (pulang kulay), habang ang function ay hindi tinukoy sa ituro ang sarili:

Kung may pagdududa, kumuha ng ilang x value at isaksak ang mga ito sa function (pag-alala na sinisira ng module ang posibleng minus sign) at suriin ang graph.

Suriin natin ang function para sa pagpapatuloy nang analytical:

1) Ang function ay hindi tinukoy sa punto, kaya maaari naming agad na sabihin na ito ay hindi tuloy-tuloy dito.

2) Itatag natin ang likas na katangian ng discontinuity;

Ang mga one-sided na limitasyon ay may hangganan at iba, na nangangahulugan na ang function ay dumaranas ng discontinuity ng unang uri na may isang pagtalon sa punto . Tandaan muli na kapag naghahanap ng mga limitasyon, hindi mahalaga kung ang function sa break point ay tinukoy o hindi.

Ngayon ang lahat na natitira ay upang ilipat ang pagguhit mula sa draft (ito ay ginawa na parang sa tulong ng pananaliksik ;-)) at kumpletuhin ang gawain:

Sagot: ang function ay tuloy-tuloy sa buong linya ng numero maliban sa punto kung saan ito ay dumaranas ng discontinuity ng unang uri na may isang pagtalon.

Minsan kailangan nila ng karagdagang indikasyon ng discontinuity jump. Ito ay kinakalkula nang simple - mula sa tamang limitasyon kailangan mong ibawas ang kaliwang limitasyon: , iyon ay, sa break point ang aming function ay tumalon ng 2 unit pababa (tulad ng sinasabi sa amin ng minus sign).

Halimbawa 3

I-explore ang function para sa pagpapatuloy. Tukuyin ang katangian ng mga discontinuities ng function, kung mayroon sila. Gumawa ng isang guhit.

Ito ay isang halimbawa para malutas mo nang mag-isa, isang halimbawang solusyon sa pagtatapos ng aralin.

Lumipat tayo sa pinakasikat at laganap na bersyon ng gawain, kapag ang function ay binubuo ng tatlong bahagi:

Halimbawa 4

Suriin ang isang function para sa pagpapatuloy at i-plot ang isang graph ng function .

Solusyon: malinaw na ang lahat ng tatlong bahagi ng function ay tuluy-tuloy sa kaukulang mga agwat, kaya nananatili itong suriin lamang ang dalawang punto ng "junction" sa pagitan ng mga piraso. Una, gumawa tayo ng isang draft na pagguhit; Nagkomento ako sa pamamaraan ng pagtatayo sa sapat na detalye sa unang bahagi ng artikulo. Ang tanging bagay ay kailangan nating maingat na sundin ang ating mga isahan na punto: dahil sa hindi pagkakapantay-pantay, ang halaga ay kabilang sa tuwid na linya (berdeng tuldok), at dahil sa hindi pagkakapantay-pantay, ang halaga ay kabilang sa parabola (pulang tuldok):


Well, in principle, everything is clear =) Ang natitira na lang ay gawing pormal ang desisyon. Para sa bawat isa sa dalawang "pagsasama" na punto, karaniwang sinusuri namin ang 3 kundisyon ng pagpapatuloy:

ako) Sinusuri namin ang punto para sa pagpapatuloy

1)

Ang mga one-sided na limitasyon ay may hangganan at iba, na nangangahulugan na ang function ay dumaranas ng discontinuity ng unang uri na may isang pagtalon sa punto .

Kalkulahin natin ang discontinuity jump bilang pagkakaiba sa pagitan ng kanan at kaliwang limitasyon:
, ibig sabihin, ang graph ay nag-jerked up ng isang unit.

II) Sinusuri namin ang punto para sa pagpapatuloy

1) – ang function ay tinukoy sa isang naibigay na punto.

2) Maghanap ng mga one-sided na limitasyon:

– ang isang panig na limitasyon ay may hangganan at pantay, na nangangahulugang mayroong pangkalahatang limitasyon.

3) – ang limitasyon ng isang function sa isang punto ay katumbas ng halaga ng function na ito sa isang naibigay na punto.

Sa huling yugto, inililipat namin ang pagguhit sa panghuling bersyon, pagkatapos ay inilalagay namin ang pangwakas na chord:

Sagot: ang function ay tuloy-tuloy sa buong linya ng numero, maliban sa punto kung saan ito dumaranas ng discontinuity ng unang uri na may pagtalon.

Halimbawa 5

Suriin ang isang function para sa continuity at bumuo ng graph nito .

Ito ay isang halimbawa para sa independiyenteng solusyon, isang maikling solusyon at isang tinatayang sample ng problema sa pagtatapos ng aralin.

Maaari kang makakuha ng impresyon na sa isang punto ang pag-andar ay dapat na tuloy-tuloy, at sa isa pa ay dapat mayroong isang discontinuity. Sa pagsasagawa, hindi ito palaging nangyayari. Subukang huwag pabayaan ang natitirang mga halimbawa - magkakaroon ng maraming kawili-wili at mahahalagang tampok:

Halimbawa 6

Nabigyan ng function . Siyasatin ang function para sa pagpapatuloy sa mga punto. Bumuo ng isang graph.

Solusyon: at muli agad na isagawa ang pagguhit sa draft:

Ang kakaiba ng graph na ito ay ang piecewise function ay ibinibigay ng equation ng abscissa axis. Narito ang lugar na ito ay iginuhit sa berde, ngunit sa isang kuwaderno ito ay karaniwang naka-highlight sa naka-bold na may isang simpleng lapis. At, siyempre, huwag kalimutan ang tungkol sa aming mga tupa: ang halaga ay kabilang sa tangent branch (pulang tuldok), at ang halaga ay kabilang sa tuwid na linya.

Ang lahat ay malinaw mula sa pagguhit - ang pag-andar ay tuloy-tuloy sa buong linya ng numero, ang natitira lamang ay upang gawing pormal ang solusyon, na dinadala sa ganap na automation pagkatapos ng 3-4 na katulad na mga halimbawa:

ako) Sinusuri namin ang punto para sa pagpapatuloy

1) - ang function ay tinukoy sa isang naibigay na punto.

2) Kalkulahin natin ang mga one-sided na limitasyon:

, na nangangahulugang mayroong pangkalahatang limitasyon.

Kung sakali, hayaan mong ipaalala ko sa iyo ang isang maliit na katotohanan: ang limitasyon ng isang pare-pareho ay katumbas ng pare-pareho mismo. Sa kasong ito, ang limitasyon ng zero ay katumbas ng zero mismo (kaliwang kamay na limitasyon).

3) – ang limitasyon ng isang function sa isang punto ay katumbas ng halaga ng function na ito sa isang naibigay na punto.

Kaya, ang isang function ay tuloy-tuloy sa isang punto sa pamamagitan ng kahulugan ng pagpapatuloy ng isang function sa isang punto.

II) Sinusuri namin ang punto para sa pagpapatuloy

1) - ang function ay tinukoy sa isang naibigay na punto.

2) Maghanap ng mga one-sided na limitasyon:

At dito - ang limitasyon ng isa ay katumbas ng yunit mismo.

– may pangkalahatang limitasyon.

3) – ang limitasyon ng isang function sa isang punto ay katumbas ng halaga ng function na ito sa isang naibigay na punto.

Kaya, ang isang function ay tuloy-tuloy sa isang punto sa pamamagitan ng kahulugan ng pagpapatuloy ng isang function sa isang punto.

Gaya ng dati, pagkatapos ng pananaliksik ay inililipat namin ang aming pagguhit sa huling bersyon.

Sagot: ang function ay tuloy-tuloy sa mga punto.

Pakitandaan na sa kondisyon na wala kaming tinanong tungkol sa pag-aaral ng buong function para sa pagpapatuloy, at ito ay itinuturing na magandang mathematical form upang bumalangkas tumpak at malinaw ang sagot sa tanong na binigay. Sa pamamagitan ng paraan, kung ang mga kondisyon ay hindi nangangailangan sa iyo na bumuo ng isang graph, pagkatapos ay mayroon kang lahat ng karapatan na hindi bumuo nito (bagaman sa ibang pagkakataon ang guro ay maaaring pilitin ka na gawin ito).

Isang maliit na mathematical na "tongue twister" para sa paglutas nito sa iyong sarili:

Halimbawa 7

Nabigyan ng function . Siyasatin ang function para sa pagpapatuloy sa mga punto. Uriin ang mga breakpoint, kung mayroon man. Isagawa ang pagguhit.

Subukang "bigkas" ang lahat ng "mga salita" nang tama =) At iguhit ang graph nang mas tumpak, katumpakan, hindi ito magiging labis sa lahat ng dako;-)

Tulad ng naaalala mo, inirerekumenda kong agad na kumpletuhin ang pagguhit bilang isang draft, ngunit paminsan-minsan ay makakatagpo ka ng mga halimbawa kung saan hindi mo agad matukoy kung ano ang hitsura ng graph. Samakatuwid, sa ilang mga kaso, kapaki-pakinabang na maghanap muna ng isang panig na mga limitasyon at pagkatapos lamang, batay sa pag-aaral, ilarawan ang mga sanga. Sa huling dalawang halimbawa, matututunan din natin ang isang pamamaraan para sa pagkalkula ng ilang isang panig na limitasyon:

Halimbawa 8

Suriin ang function para sa continuity at buuin ang schematic graph nito.

Solusyon: ang masasamang puntos ay halata: (binabawasan ang denominator ng exponent sa zero) at (binabawasan ang denominator ng buong fraction sa zero). Hindi malinaw kung ano ang hitsura ng graph ng function na ito, na nangangahulugang mas mabuting magsaliksik muna.

Ang punto a ay tinatawag na isang punto ng naaalis na discontinuity ng isang function kung ang limitasyon ng function sa puntong ito ay umiiral, ngunit sa punto a ang function ay alinman sa hindi tinukoy o ang halaga nito ay hindi katumbas ng limitasyon sa puntong ito

Pagkagambala ng unang uri.

Ang point a ay tinatawag na discontinuity point ng unang uri ng function kung sa puntong ito ang function ay may hangganan ngunit hindi pantay na kaliwa at kanang limitasyon.

Pagkagambala ng pangalawang uri.

Ang point a ay tinatawag na discontinuity point ng pangalawang uri ng isang function. ang isang panig na limitasyon ay walang katapusan.

25. Derivative: kahulugan, mekanikal at geometriko na kahulugan. Equation ng isang tangent sa isang curve.

Kahulugan ng derivative

Hayaan ang function tinukoy sa isang tiyak na pagitan X. Bigyan natin ang halaga ng argumento sa punto ng isang arbitrary na pagtaas kaya na ang punto kabilang din sa X. Pagkatapos ay ang kaukulang pagtaas mga function ay magiging .

ODA. Ang derivative ng isang function sa isang punto ay ang limitasyon ng ratio ng pagtaas ng function sa puntong ito sa pagtaas ng argumento sa (kung umiiral ang limitasyong ito).

Kung sa ilang mga punto ang limitasyon ay walang hanggan, kung gayon ang pag-andar ay sinasabing mayroong isang walang katapusang derivative sa puntong iyon. Kung ang isang function ay may derivative sa bawat punto ng set X, kung gayon ang derivative ay isa ring function ng argument na x na tinukoy sa X.

Geometric na kahulugan ng derivative

Upang linawin ang geometric na kahulugan ng derivative, kailangan nating matukoy ang tangent sa graph ng function sa isang naibigay na punto.

Def. Ang tangent sa graph ng isang function sa point M ay ang nililimitahan na posisyon ng secant MN kapag ang point N ay may posibilidad na ituro ang M sa kahabaan ng curve.

Ang equation ng isang lapis ng mga linyang dumadaan sa isang punto ay may anyo

Ang angular coefficient ng secant ay katumbas ng

Pagkatapos ang slope ng tangent ay katumbas ng

Mula dito ay sumusunod ang isang malinaw na konklusyon na . Ito ang ano geometric na kahulugan ng derivative.

mula dito, v(t 0)= x'(t 0) , ibig sabihin. ang bilis ay ang hinango ng isang coordinate na may kinalaman sa oras. Ito ang ano mekanikal na kahulugan derivative . Gayundin, ang acceleration ay ang derivative ng bilis na may paggalang sa oras: O.I. Besov. Mga lektura sa pagsusuri sa matematika. Bahagi 1. Moscow, 2004. = v'(t).

Tangent equation sa graph ng isang function sa isang punto ay may anyo:

26. Mga pangunahing tuntunin ng pagkita ng kaibhan. Mga derivative ng mga pangunahing pag-andar ng elementarya.

Mga tuntunin ng pagkita ng kaibhan.

1. Ang derivative ng isang pare-pareho ay zero

2. Ang derivative ng argumento ay katumbas ng isa.

3. Ang derivative ng isang algebraic sum ng isang finite number of differentiable functions ay katumbas ng parehong sum ng derivatives ng mga function na ito.

Ang derivative ng produkto ng dalawang differentiable function ay katumbas ng produkto ng derivative ng unang factor at ang pangalawa kasama ang produkto ng unang factor at ang derivative ng pangalawa.

Corollary 1. Maaaring alisin ang pare-parehong salik sa tanda ng derivative.

Corollary 2. Ang derivative ng produkto ng ilang differentiable function ay katumbas ng kabuuan ng mga produkto ng derivative ng bawat isa sa mga salik ng lahat ng iba pa, halimbawa

5. Ang derivative ng quotient ng dalawang differentiable function ay matatagpuan gamit ang formula:

Mga derivative ng mga pangunahing pag-andar ng elementarya.

1. (C)” = 0, kung saan ang C = const

2. (x a)” = ax a-1 , kung saan ang a ay hindi katumbas ng 0

3. (a x)” = a x ln a, kung saan a > 0

4. (e x)” = e x

5. (log a x)” =1/x ln a, kung saan a > 0

6. (ln x)” =1/x

7. (sin x)” = cos x

8. (cos x)” = - sin x

9. (tg x)” =1/cos 2 x

10. (ctg x)” = -1/sin 2 x

11. (arcsin x)” = 1/~1-x 2

12. (arccos x)’ = -1/~1-x 2

13. (arctg x)” =1/1+x 2

14. (arcctg x)” = -1/1+x 2

27. Derivative ng isang kumplikadong function. Derivatives ng mas mataas na mga order.